Modeling Volcanic Processes The Physics And Mathematics Of Volcanism Pdf
Abstract
Magma from Plinian volcanic eruptions contains an extraordinarily large numbers of bubbles. Nucleation of those bubbles occurs because pressure decreases as magma rises to the surface. As a consequence, dissolved magmatic volatiles, such as water, become supersaturated and cause bubbles to nucleate. At the same time, diffusion of volatiles into existing bubbles reduces supersaturation, resulting in a dynamical feedback between rates of nucleation due to magma decompression and volatile diffusion. Because nucleation rate increases with supersaturation, bubble number density (BND) provides a proxy record of decompression rate, and hence the intensity of eruption dynamics. Using numerical modeling of bubble nucleation, we reconcile a long-standing discrepancy in decompression rate estimated from BND and independent geospeedometers. We demonstrate that BND provides a record of the time-averaged decompression rate that is consistent with independent geospeedometers, if bubble nucleation is heterogeneous and facilitated by magnetite crystals.
Introduction
Plinian eruptions are among Earth's most explosive volcanic events and are typically associated with magmas of high-silica content1. In the past 100 kyr over 500 Plinian silicic eruptions with Volcanic Explosivity Index of four or greater have occurred globally2 (Fig. 1a). These eruptions have considerable destructive power and present extensive risks, both locally (e.g., pyroclastic density current) and globally (e.g., atmospheric ash and aerosol dispersal). The destructive potential of such eruptions derives from numerous bubbles that nucleate and grow during magma ascent3,4. These bubbles contain a highly compressible fluid mixture of exsolved magmatic volatiles, predominantly H2O 5. Bubble overpressure, relative to the surrounding melt, provides the potential energy for magma fragmentation, which results in explosive eruptions6. The development of overpressure in bubbles is thought to depend on the rate at which magma decompresses during ascent7,8. Because eruptive processes are inaccessible to direct observation, understanding explosive volcanism is contingent upon reconstructing governing processes and their controlling parameters from indirect observations. The number density of bubbles, preserved in erupted pyroclasts, is such an independent observation and of critical importance to elucidating the dynamical feedback between magma decompression, H2O exsolution, and explosive magma fragmentation.
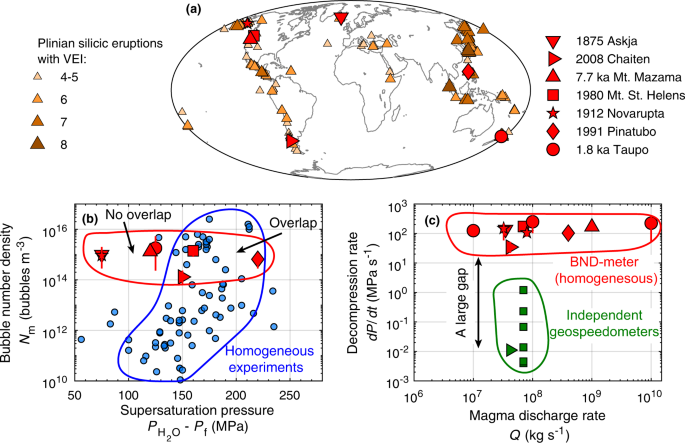
a Spatial distribution of Plinian (Volcanic Explosivity Index ≥ 4) silicic eruptions over the past 100 kyr, based on Crosweller et al.2. Red symbols are eruptions for which bubble number density and H2O saturation pressure are documented. They are: 1875 Askja40,41; 2008 Chaiten42,43; 7.7 ka Mount Mazama44,45; 1980 Mount St. Helens (MSH)46,47,48; 1912 Novarupta49,50; 1991 Pinatubo51,52; 1.8 ka Taupo53 eruptions. b Bubble number density versus the maximum potential H2O supersaturation pressure for eruptions (red symbols) and for homogeneous nucleation experiments (blue symbols)10,12,19,32,54,55,56,57,58,59. Only experiments with supersaturation pressure of ≥150 MPa overlap with eruptions. c Decompression rate values estimated from observed bubble number density and homogeneous nucleation17. There is a large gap between these estimates and those calculated by independent geospeedometers for the same eruptions43,60,61,62,63,64.
Full size image
Bubble nucleation rate and the resultant bubble number density are governed by the feedback between H2O exsolution and magma decompression4. The latter is a consequence of the combined decrease in static pressure and pressure loss from viscous resistance to flow as magma rises toward the surface6. Consequently, decompression rate depends dynamically on magma discharge rate, conduit dimensions, and magma viscosity, which increases as H2O exsolves into bubbles by diffusion9. The efficiency of diffusion, in turn, is rate limited by the number density of bubbles, such that slow diffusion kinetics facilitates large supersaturations and high rates of bubble nucleation4. Bubble number density provides a record of this feedback. Reconstruction of these processes and reliable estimation of magma decompression rate require quantitative models of bubble nucleation that are calibrated with experiments.
Bubble number densities preserved in pyroclasts from Plinian silicic eruptions span a narrow range of 1015 ± 1 m−3 despite more than 3 wt% variation in pre-eruptive H2O concentrations (Fig. 1b). Figure 1b compares the observed bubble number densities with experimental results of homogeneous nucleation. The data are presented in terms of the potential maximum supersaturation pressure. In case of experiments, it is the difference between the H2O saturation pressure and the final pressure, whereas for eruptions, it is the difference between saturation pressure and atmospheric pressure. Homogeneous nucleation typically initiates at supersaturation pressures of ≈110 MPa10. Bubble number density increases with supersaturation pressure and reaches the range of bubble number density observed in pyroclasts at supersaturation pressures of >150 MPa. Such high pressures, however, are greater than the potential maximum supersaturation pressure for most eruptions11. Moreover, the conventional estimates of decompression rate based on homogeneous nucleation are unrealistically high (~100 MPa s−1), do not correlate with magma discharge rate, and are substantially greater than estimates from independent geospeedometers, which are ≤1 MPa s−1 (Fig. 1c). To resolve these discrepancies, Shea11 hypothesized that bubble nucleation is perhaps heterogeneous and facilitated by abundant pre-existing crystals. The heterogeneous nucleation hypothesis, however, does not close the gap between decompression rate estimates from bubble number density and independent geospeedometers.
The purpose of this study is to reconcile observed bubble number densities in Plinian silicic eruptions with independent geospeedometers. We integrate Hajimirza et al.'s12 bubble nucleation model, obtained by calibrating classical nucleation theory against experiments, with a model of magma flow in the conduit during Plinian eruptions4,13,14. We find that the vast majority of eruptions require heterogeneous nucleation, perhaps due to the presence of magnetite crystals. This is consistent with Shea's hypothesis11. We assess the implications of heterogeneous bubble nucleation on the conduit flow, with a focus on magma decompression rates. Conduit flow models indicate that the decompression rate during magma ascent is not constant. Rather it increases as H2O exsolves and viscosity increases6,15. Our model simulations account for this time-dependent magma decompression and are more consistent with the fluid dynamics of magma ascent. This allows for the estimation of a time-averaged decompression rate, defined as the ratio of total decompression over total ascent time. The time-averaged decompression rate is well suited for comparison with independent geospeedometers, which yield decompression rate estimates within close range of the time-averaged values16. In contrast, estimates based on scaling relations, such as BND meter of Toramaru17 which is widely used11, yields values that are more representative of decompression rates at the peak of nucleation11 and can be orders of magnitude higher than time-averaged estimates. By accounting for the aforementioned time-dependent feedback during magma decompression, we find that the time-averaged decompression rates estimated from BND under heterogeneous nucleation are consistent with independent geospeedometers.
Results
Bubble nucleation
Bubble nucleation is the formation of molecular clusters that are larger than a critical size and stable to grow into bubbles. Nucleation is driven by thermodynamic disequilibrium due to supersaturation of dissolved volatiles, as magma decompresses to a pressure below its saturation pressure. The change in free energy, W, associated with the formation of bubble nuclei is quantified by classical nucleation theory18. W derives from the balance between a reduction in free energy, caused by the clustering of volatile molecules, and an increase in free energy, caused by the formation of a new interface between molecules within the cluster and the surrounding silicate. The bubble nucleation rate depends exponentially on W 18. Bubble nuclei are of the order of a few nanometers in size12,18 and will grow into micron- to millimeter-size bubbles by diffusion, which tends to reduce supersaturation.
We simulate bubble nucleation and growth during magma decompression in order to examine the conditions under which bubbles in Plinian pyroclasts may have nucleated (see "Methods" section for details). We consider H2O as the dominant volatile phase because it is the most abundant5 and primarily controls the final bubble number density4. Our simulations predict nucleation rate during decompression from an initial saturation pressure until magma fragmentation. Decompression rate is estimated for steady flow of magma within a cylindrical conduit of constant cross-sectional area using the Darcy–Weisbach relation6. Dependent parameters are: pressure in the surrounding melt, average concentration of dissolved H2O in the melt, nucleation rate, bubble number density, average bubble size, pressure inside bubbles, and bubble volume fraction. We use the nucleation model of Hajimirza et al.12, which has been calibrated against homogeneous bubble nucleation experiments in rhyolite, and reliably predicts experimental results over a wide range of saturation pressures and decompression rates.
The homogeneous nucleation energy, W Hom, is large and a high supersaturation pressure is required to overcome the surface energy barrier for nucleus formation10,12. In our simulations, we first examined whether the observed bubble number density in each eruption can be produced by homogeneous nucleation. We find that the 1991 eruption of Pinatubo is the only eruption where the observed bubble number density can be attained by homogeneous nucleation. For all other eruptions a necessary reduction in nucleation energy, relative to the homogeneous value, is required. This reduction could be attained by the presence of dissolved fluorine. For example, 1 wt% fluorine reduces nucleation energy by 75%19. Typical fluorine concentrations in explosively erupted magmas, however, are only ~200–1500 ppm5. An alternative is heterogeneous nucleation on crystals18, including nanometer-size nanolites11. Here we assess the effect of heterogeneous nucleation on magma ascent dynamics during Plinian eruptions.
Reconciling bubble nucleation with eruption dynamics
Heterogeneous nucleation in magmatic systems is facilitated by the presence of crystalline molecular aggregates that provide nucleation sites for bubbles. Heterogeneous nucleation facilitates nucleation by reducing the homogeneous nucleation energy by a factor, 0 <α < 1. The value of α during such heterogeneous nucleation is described as a function of the dihedral contact angle, θ, between the melt-bubble interface and the pre-existing crystal (Fig. 2). Direct measurements of θ for bubble nuclei are impossible because nuclei are too small and ephemeral. Some studies have attempted to estimate θ from the contact angle between microscopically observed bubbles and crystals20. It is, however, unlikely that the contact angle is the same for nuclei and microscopically observable bubbles because their thermodynamic properties are different12,18. Instead, θ has been inferred from the difference in pressure, ΔP, at which bubbles first nucleate during decompression in homogeneous and heterogeneous nucleation experiments, with \(\alpha \,=\,{({{\Delta }}{P}_{{\rm{Het}}}/{{\Delta }}{P}_{{\rm{Hom}}})}^{2}\) 18,21. Based on such experiments it has been shown that the contact angle is dependent on the substrate's mineralogical structure (Fig. 2). For example, the contact angle for feldspar is ~0–20°20, for pyroxene is 40–60°22, whereas for hematite is ~90–100°21,23, and for magnetite is ~145–160°20,21. The contact angles for feldspar and pyroxene are too low to allow heterogeneous nucleation to match the observed bubble number densities (Fig. 2). Nucleation on hematite can match observed bubble number densities in most eruptions. To the best of our knowledge, however, hematite does not occur naturally in most magmas. Magnetite is the most effective mineral phase for heterogeneous bubble nucleation and is the only mineral phase that can cause heterogeneous nucleation to produce bubbles in sufficient numbers in all eruptions considered.
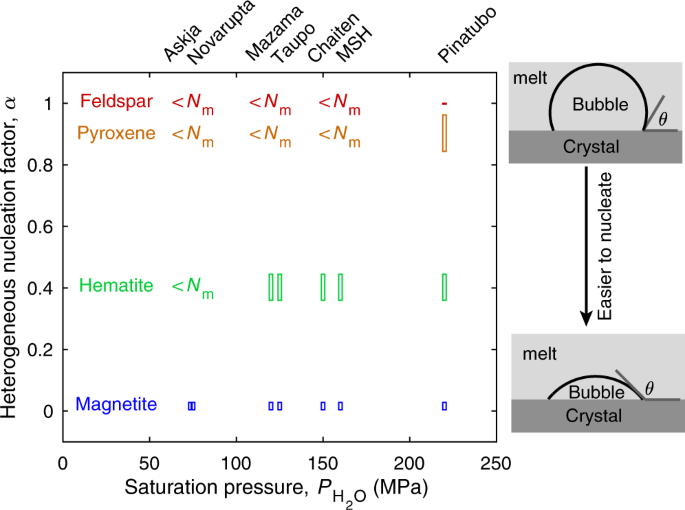
Heterogeneous nucleation factor, α, required for each eruption to match bubble number densities. Pinatubo can be reconciled with homogeneous nucleation (α = 1), whereas all other eruptions require heterogeneous nucleation (α < 1). α shown are for magnetite20,21, hematite21,23, pyroxene22, and feldspar20. Magnetite is the only mineral phase that allows heterogeneous nucleation to simultaneously match observed bubble number densities in all eruptions.
Full size image
For each eruption we ran simulations wherein homogeneous nucleation energy is scaled with α for the range of possible contact angles for magnetite (145–160°). The simulation parameters are given in Supplementary Table 1. The time-averaged decompression rates, at which the magma would be predicted to fragment with a bubble number density equal to each eruption, range between 0.1 and 1 MPa/s (Fig. 3). These estimates reconcile observed bubble number densities with nucleation theory and the fundamental fluid dynamics of magma ascent6. The time-averaged decompression rates are more than one order of magnitude lower than equivalent values predicted by the BND meter for heterogeneous nucleation17. The reason for this discrepancy is because decompression rates from the BND meter are representative of peak rates. This is an important distinction because independent geospeedometers, which tend to be based on diffusion kinetics, provide estimates that closely approximate time-averaged values16. Thus, the time-averaged decompression rates obtained from our simulations largely eliminate the gap with independent geospeedometers (Fig. 3). Despite heterogeneous nucleation generating sufficient numbers of bubbles at more realistic slower decompression rates, those rates still exceed geospeedometer estimates, which we speculate to be indicative of a widening conduit with depth.
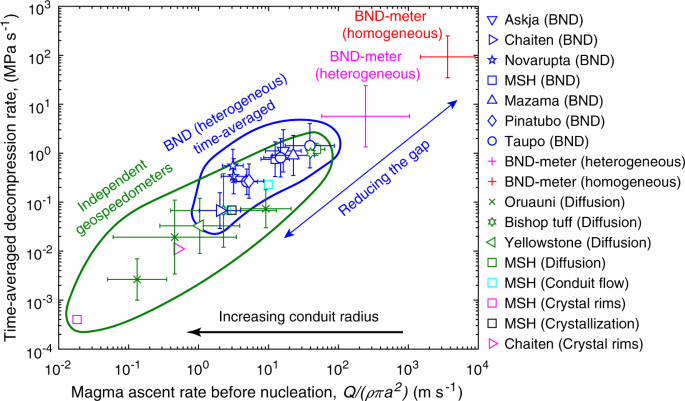
The blue symbols show the time-averaged estimates from bubble number density with heterogeneous nucleation on magnetite. The error bars represent uncertainties in magnetite contact angle. Heterogeneous nucleation substantially reduces the gap in decompression rate between homogeneous nucleation and independent geospeedometers that include: diffusion in melt inclusions and melt embayments for May 18th, 1980 Mt. St. Helens60, 0.77 Ma Bishop tuff65,66, 27 ka Oruauni66,67,68, and 2 Ma Yellowstone66; conduit models for May 18th, 1980 Mt. St. Helens61,62; crystal rims for May 18th, 1980 Mt. St. Helens63 and 2008 Chaiten43; and groundmass crystallization for May 18th, 1980 Mt. St. Helens64.
Full size image
Discussion
Our simulation results suggest that bubble number densities can be reconciled with pre-eruptive H2O concentration and independent geospeedometers, if nucleation is heterogeneous due to magnetite. For none of the eruptions magnetite crystals have been reported at number densities similar to or greater than bubble number densities. This does not, however, rule out the presence of magnetite because they are typically much smaller than bubbles and might be undercounted in 2D scanning electron microscopy (SEM) images11,24. Furthermore, magnetite crystals might exist at sizes well below the resolution of SEM images. For example, magnetite nanolites as small as 20 nm are reported in samples from Paintbrush Tuff (USA)25, and are discovered in samples from Green Tuff (Italy) and Yellowstone (USA) using Raman spectroscopy26,27. Using transmission electron microscopy, Mujin et al.24 observed magnetite nanolites in samples from Shinmoedake Volcano (Japan) with sizes down to 1 nm and number densities of up to ~1023 m−3.
Our analysis is based on the hypothesis that heterogeneous nucleation sites exist during eruptive magma ascent. This is supported by the fact that bubble nucleation experiments require extensive treatment at superliquidus conditions in order to avoid heterogeneous nucleation, in some cases without observable crystals20,28. The hypothesized existence of abundant oxides in erupting magmas at subliquidus conditions is thus not unreasonable11. By the same token, homogeneous bubble nucleation experiments, while necessary as a basis for understanding nucleation, may not fully encapsulate bubble formation in volcanic eruptions.
Heterogeneous nucleation exerts a complex feedback between H2O exsolution, decompression rate, and explosive magma fragmentation. Figure 4 provides a representative example of model results. Heterogeneous nucleation starts shortly after magma decompression. After the onset of nucleation H2O diffuses into the existing bubbles. Bubbles grow, resulting in progressive decrease of the characteristic diffusion length, which enhances the diffusion of H2O into bubbles. The average dissolved H2O concentration therefore remains close to equilibrium as the magma continues to decompress. The initial decompression rate is predominantly due to the reduction in hydrostatic pressure, which is proportional to magma ascent rate. As more H2O exsolves magma viscosity increases resulting in a continuous increase in decompression rate. Consequently supersaturation gradually increases, resulting in a second nucleation peak of higher rate than the first one. Because of the substantial overpressure in the newly nucleated bubbles, fragmentation conditions are reached immediately after the second nucleation peak. Our simulations predict that under heterogeneous nucleation a second nucleation peak occurs for all eruptions, independent of their saturation pressure. The detailed simulation results for all eruptions are given in Supplementary Table 2.
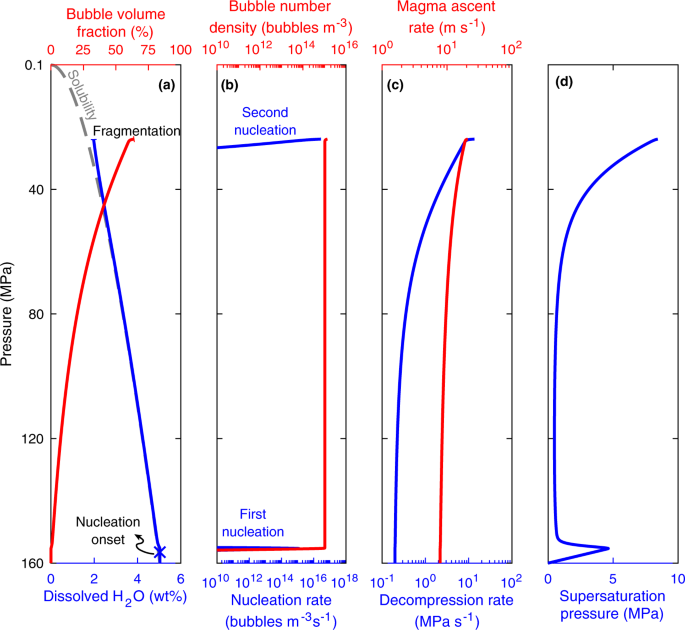
The contact angle is θ = 160° (α = 0.003). Nucleation first occurs at low supersaturation. Subsequently H2O concentration remains close to equilibrium because of H2O diffusion into nucleated bubbles. This results in a progressive increase in viscosity and hence decompression rate. Supersaturation pressure increases gradually, leading to a second nucleation peak, followed by magma fragmentation.
Full size image
In summary, we find that bubbles at number densities in pyroclastic samples from a wide range of Plinian silicic eruptions are consistent with heterogeneous nucleation due to magnetite, if present at number densities similar to those discovered in several explosive eruptions24,25,26,27. Such heterogeneous bubble nucleation can resolve the discrepancy between the inferred water saturation for many eruptions and that required to nucleate bubbles. By accounting for the time-varying decompression rate, arising due to feedbacks between H2O exsolution and magma viscosity, we overcome the peak decompression rate bias of conventional methods. We thus calculate time-averaged decompression rates that can be compared to independent geospeedometers. We find that heterogeneous nucleation largely closes the gap with independent geospeedometers. Heterogeneous bubble nucleation due to magnetite is a viable hypothesis that provides impetus for future investigations, in particular a systematic search for the presence of magnetite nanolites in Plinian samples.
Methods
Model assumptions
We simulated bubble nucleation and growth during magma ascent in a vertical cylindrical conduit with a constant cross-sectional area. For a given eruption, simulations commence from H2O saturation pressure and stop when fragmentation conditions are met.
The assumption for magma flow in the conduit are: steady state because the time scale for Plinian eruptions is substantially longer than the time scale of magma ascent in the conduit29; one-dimensional flow with flow properties averaged over the cross-sectional area of the conduit6; the relative velocity between bubbles and melt is neglected because the drag force associated with silicic melt prevents bubbles from rising independently through the melt15; isothermal conditions and nucleation is only driven by decompression14; nanolites do not affect magma rheology; nucleation after fragmentation is assumed to be negligible14.
The assumptions for bubble nucleation and growth are: magma is initially bubble free; H2O exsolution is non-equilibrium; bubble nucleation rate is estimated using classical nucleation theory; nucleation is heterogeneous on abundant pre-existing magnetite crystals (no crystal nucleation); we use the method of moments to estimate the growth rate of bubbles with different sizes4; we assume bubble growth is steady state4. This is justified because the inertia terms in the diffusion equation are negligible at low supersaturation pressures during heterogeneous nucleation30.
Magma flow in the conduit
Considering the above assumptions, conservation of mass and momentum simplifies to
$$\frac{\partial (\rho U)}{\partial z}\,=\,0,$$
(1)
and
$$\rho U\frac{\partial U}{\partial z}\,=\,-\frac{\partial {P}_{{\rm{m}}}}{\partial z}\,-\,\rho g\,-\,{F}_{{\rm{fric}}},$$
(2)
respectively. Here ρ is magma density, averaged over melt and gas phases,
$$\rho \,=\,\phi {\rho }_{{\rm{g}}}\,+\,(1\,-\,\phi ){\rho }_{{\rm{m}}}.$$
(3)
ϕ is the volume fraction of bubbles, ρ g and ρ m are gas and melt densities, respectively, U is magma ascent rate, g is the gravitational acceleration, and F fric is the pressure loss due to friction forces. The latter is calculated from the Darcy–Weisbach relation, F fric = 8μ U/a 2. a is the conduit radius and μ is the magma viscosity, given by \({\mu }_{{\rm{m}}}{(1\,-\,{\phi }_{{\rm{crystal}}}/0.6)}^{(-5/2)}\). Here μ m is the melt viscosity and ϕ crystal is the volume fraction of microlites. Substituting Eq. (1) into Eq. (2) and replacing U with Q/(ρ π a 2) gives the pressure loss as
$$\frac{\partial {P}_{{\rm{m}}}}{\partial z}\,=\,-\left(\rho g+\frac{Q}{\rho \pi {a}^{2}}\left(\frac{8\mu }{{a}^{2}}\,-\,\frac{Q}{\rho \pi {a}^{2}}\frac{\partial \rho }{\partial z}\right)\right),$$
(4)
where Q is the mass discharge rate.
Bubble nucleation
In our model, we allow for non-equilibrium exsolution, that is H2O may become supersaturated as magma decompresses, driving bubble nucleation and growth. We used classical nucleation theory to estimate nucleation rate of stable bubble nuclei at a given supersaturation pressure. Molecular clusters of volatiles are stable and grow into bubbles if they are larger than the critical nucleus size, R c, given by18
$${R}_{{\rm{c}}}\,=\,\frac{2\gamma }{{P}_{{\rm{n}}}\,-\,{P}_{{\rm{m}}}},$$
(5)
where γ is the surface tension of bubble nuclei, P n is the pressure inside a bubble nucleus, and P m is pressure in the surrounding melt. P n is related to the saturation pressure of volatiles, P sat, through23
$$f({P}_{{\rm{n}}},T){P}_{{\rm{n}}}\,=\,f({P}_{{\rm{sat}}},T){P}_{{\rm{sat}}}{e}^{{{\Omega }}({P}_{{\rm{m}}}\,-\,{P}_{{\rm{sat}}})/{k}_{{\rm{B}}}T},$$
(6)
where T is temperature, f(P, T) is the fugacity coefficient of the supersaturated volatile phase, Ω is the volume of volatile molecules, and k B is the Boltzmann constant. The homogeneous nucleation energy, W Hom, is estimated from
$${W}_{{\rm{Hom}}}\,=\,\frac{16\pi {\gamma }^{3}}{3{({P}_{{\rm{n}}}\,-\,{P}_{{\rm{m}}})}^{2}},$$
(7)
and the nucleation rate is18,31
$$J\,=\,{J}_{0}\exp \left(-\frac{{W}_{{\rm{Hom}}}}{{k}_{{\rm{B}}}T}\alpha \right),$$
(8)
with
$${J}_{0}\,=\,\frac{2{{\Omega }}{n}_{0}^{2}D}{{a}_{0}}\sqrt{\frac{\gamma }{{k}_{{\rm{B}}}T}}.$$
(9)
n 0 is the concentration of volatiles molecules in the melt, D is the diffusion coefficient, a 0 is the average distance between volatiles molecules and α is the heterogenous nucleation factor, which depends on the contact angle, θ, between bubble nuclei and crystals as
$$\alpha \,=\,\frac{(2\,\,-\cos \theta ){(1\,+\,\cos \theta )}^{2}}{4}.$$
(10)
The nucleation rate is strongly controlled by surface tension, γ, such that a few percent variations in γ can change J by >10 orders of magnitude32. A reliable prediction of nucleation rate, and consequently bubble number density, thus requires a firm constraint on surface tension. Here we use the surface tension formulation defined by Hajimirza et al.12, which has been shown to reliably predict observed bubble number density in homogeneous nucleation experiments . γ is given by
$$\gamma \,=\,\frac{0.49\,{\gamma }_{{\rm{B}}}}{1\,+\,2\delta /{R}_{{\rm{c}}}},$$
(11)
where γ B is the surface tension measurements for macroscopic bubbles33, and δ ≈ 0.32 nm is the Tolman length for bubble nuclei in rhyolite12,34.
Bubble growth
When a bubble nucleus forms, the H2O concentration at the bubble-melt interface is determined by the solubility of H2O at the pressure inside the bubble. This concentration is lower than the concentration in the surrounding melt, resulting in a concentration gradient which drives diffusion of H2O molecules toward bubble nuclei. The resultant mass flux of H2O into a bubble, q, is approximated as,
$$q\,=\,D{\left(\frac{\partial c}{\partial r}\right)}_{r \,=\, R}.$$
(12)
Here D is diffusion coefficient, r is the distance from bubble's center, R is bubble radius, and c is the water concentration in the surrounding melt, given by7
$$\frac{\partial c}{\partial t}\,+\,\frac{dR}{dt}\frac{\partial c}{\partial z}\,=\,\frac{1}{{r}^{2}}\frac{\partial c}{\partial r}\left(D{r}^{2}\frac{\partial c}{\partial r}\right).$$
(13)
Chernov et al.30 demonstrated that at low supersaturation pressures the inertial terms, the left-hand side in Eq. (13), are negligible. We thus neglect those terms because in heterogeneous nucleation supersaturation pressure remains low. With boundary conditions c(r =R) =C R and c(r →∞) =C m, where C m and C R are the average H2O concentrations in the melt and at the bubble-melt interface, respectively, c is estimated as30
$$c\,=\,{C}_{{\rm{m}}}\,-\,({C}_{{\rm{m}}}\,-\,{C}_{{\rm{R}}})\frac{R}{r}.$$
(14)
The mass of H2O inside the bubble, m b, will increase due to diffusion at a rate
$$\frac{d{m}_{{\rm{b}}}}{dt}\,=\,4\pi {R}^{2}{\rho }_{{\rm{m}}}q.$$
(15)
The bubble growth rate is given by
$$\frac{dR}{dt}\,=\,\frac{R}{4\mu }\left({P}_{{\rm{b}}}\,-\,{P}_{{\rm{m}}}\,-\,\frac{2\gamma }{R}\right),$$
(16)
which accounts for bubble growth driven by diffusion as well as decompression. Here μ is the viscosity of melt surrounding the bubble, P b is the pressure inside the bubble, estimated using the equation of state of H2O, and d/d t =U∂/∂z is the material derivative of a given quantity in steady state. Inertial terms in Eq. (16) are neglected, given that they are considerably smaller than the viscous terms4.
The above equations describe the growth rate of a single bubble. Because the number of bubbles in the magma is too high to track growth rates for each individual bubble, we use the method of moments, which calculates the moments of size distributions. The kth moment is defined as4
$${M}_{k}(t)\,=\,\mathop{\int}\nolimits_{0}^{\infty }{R}^{k}{{\Lambda }}\left(R, t\right)\ dR,$$
(17)
where Λ is number of bubbles with radii in the interval of R and R +d R per unit volume of melt. Each moment refers to a measurable characteristic quantity4: M 0 is the total number of bubbles per unit volume of melt (BND), M 1 is the total radius of bubbles per unit volume of melt, 4π M 2 is the total surface area of bubbles per unit volume of melt, and \(\frac{4\pi }{3}{M}_{3}\) is the total volume of bubbles per unit volume of melt. The volume fraction of bubbles in Eq. (3) is estimated from \((\frac{4\pi }{3}{M}_{3})/(1\,+\,\frac{4\pi }{3}{M}_{3})\).
The evolution of bubble size distribution due to the growth of existing bubbles and nucleation of new bubbles is given by the population balance equation as13
$$\frac{d{{\Lambda }}(R,t)}{dt}\,+\,G(\hat{R})\frac{\partial \left({{\Lambda }}(R,t)\right)}{\partial R}\,=\,J\mathop{\int}\nolimits_{0}^{\infty }\delta (R\,-\,{R}_{{\rm{c}}})\ dR.$$
(18)
δ is the Dirac delta function and \(G(\hat{R})\) is the growth rate of bubbles, assumed to be equal for all bubbles and estimated from Eq. (16) for a bubble of mean radius, \(\hat{R}\,=\,{M}_{1}/{M}_{0}\). The evolution of the zeroth moment through time is given by
$$\frac{d{M}_{0}}{dt}\,=\,J,$$
(19)
and the evolution of the higher-order moments, k ≥ 1, is given by
$$\frac{d{M}_{k}}{dt}\,=\,kG(\hat{R}){M}_{k\,-\,1}\,+\,J{R}_{{\rm{c}}}^{k}.$$
(20)
The concentration of H2O dissolved within the melt decreases as a result of the diffusion of water into bubbles. Mass conservation of H2O requires that
$$\frac{d{C}_{{\rm{m}}}}{dt}\,=\,-\frac{1}{{\rho }_{m}}\left({M}_{0}\frac{d{m}_{{\rm{b}}}}{dt}\,+\,J{m}_{{\rm{c}}}\right),$$
(21)
where ρ m is the melt density, assumed to be constant throughout magma decompression, and m c is the mass of a bubble nuclei estimated from the equation of state.
Model simulation
For each eruption, we integrated Eqs. (4, 19, and 20) for k = 1 through 3, as well as Eq. (21), using the ode15s function of MATLAB®. Each simulation initiated at the known saturation pressure and with additional initial conditions of
$${M}_{k}\,=\,0,\quad {P}_{{\rm{m}}}\,=\,{P}_{{{\rm{H}}}_{2}{\rm{O}}}\quad {\rm{and}}\quad {C}_{{\rm{m}}}\,=\,{C}_{{{\rm{H}}}_{2}{\rm{O}}},$$
(22)
where \({C}_{{{\rm{H}}}_{2}{\rm{O}}}\) is related to \({P}_{{{\rm{H}}}_{2}{\rm{O}}}\) through the H2O solubility relation35. A given simulation ends when the fragmentation criterion of Papale36 is reached. The values of input variables for each eruption are given in Supplementary Table 1.
The objective of our model simulation is to estimate decompression rate, conditional on the observational constraints of measured bubble number density and magma fragmentating. All parameters in the governing system of equations are either specified or calculated from existing formulations: H2O solubility35, diffusion coefficient37, equation of state38, fugacity coefficient38, surface tension12, melt viscosity9, and the molecular volume of H2O39. Conduit radius, which is related to decompression rate through equation (4), is the only parameter that is not constrained. For each eruption, the model simulations predict a conduit radius and an average decompression rate that are conditional on the aforementioned observational constraints. The values of output variables for each eruption are given in Supplementary Table 2.
Data availability
The authors declare that the data that support the findings of this study are available within the paper and the supplementary tables.
Code availability
All equations used in the code are presented in the "Methods" section. The code is available at "https://github.com/Sahand-Hajimirza/BND-speedometer".
References
- 1.
Carey, S. & Sigurdsson, H. The intensity of plinian eruptions. Bull. Volcanol. 51, 28–40 (1989).
ADS Article Google Scholar
- 2.
Crosweller, H. S. Global database on large magnitude explosive volcanic eruptions (LaMEVE). J. Appl. Volcanol. 1, 1–13 (2012).
Article Google Scholar
- 3.
Sparks, R. S. J. The dynamics of bubble formation and growth in magmas: a review and analysis. J. Volcanol. Geother. Res. 3, 1–37 (1978).
ADS CAS Article Google Scholar
- 4.
Toramaru, A. Numerical study of nucleation and growth of bubbles in viscous magmas. J. Geophys. Res. 100, 1913–1931 (1995).
ADS Article Google Scholar
- 5.
Wallace, P. J., Plank, T., Edmonds, M. and Hauri, E. H. Volatiles in magmas. in The Encyclopedia of Volcanoes 2nd edn, (eds Sigurdsson, H. Houghton, B., McNutt, S., Hazel, R. & Stix, J) Ch. 3, 163 – 183 (Academic Press, Amsterdam, 2015).
- 6.
Wilson, L., Sparks, R. S. J. & Walker, G. P. L. Explosive volcanic eruptions – IV. The control of magma properties and conduit geometry on eruption column behaviour. Geophys. J. Int. 63, 117–148 (1980).
ADS Article Google Scholar
- 7.
Gonnermann, H. M. and Manga, M. Dynamics of magma ascent. in Modeling Volcanic Processes: The physics and Mathematics of Volcanism (eds Fagents, S. A., Gregg, T. K. P. & Lopes, M. C.) 55–84 (Cambridge University Press, Cambridge, UK, 2013).
- 8.
Cassidy, M., Manga, M., Cashman, K. V. & Bachmann, O. Controls on explosive-effusive volcanic eruption styles. Nat. Commun. 9, 2839 (2018).
ADS PubMed PubMed Central Article CAS Google Scholar
- 9.
Hui, H. & Zhang, Y. Toward a general viscosity equation for natural anhydrous and hydrous silicate melts. Geochim. Cosmochim. Acta 71, 403–416 (2007).
ADS CAS Article Google Scholar
- 10.
Mangan, M. T. & Sisson, T. Delayed, disequilibrium degassing in rhyolite magma: decompression experiments and implications for explosive volcanism. Earth Planet. Sci. Lett. 183, 441–455 (2000).
ADS CAS Article Google Scholar
- 11.
Shea, T. Bubble nucleation in magmas: a dominantly heterogeneous process. J. Volcanol. Geotherm. Res. 343, 155–170 (2017).
ADS CAS Article Google Scholar
- 12.
Hajimirza, S., Gonnermann, H. M., Gardner, J. E. & Giachetti, T. Predicting homogeneous bubble nucleation in rhyolite. J. Geophys. Res. 124, 2395–2416 (2019).
ADS CAS Article Google Scholar
- 13.
Toramaru, A. Measurement of bubble size distributions in vesiculated rocks with implications for quantitative estimation of eruption processes. J. Volcanol. Geotherm. Res. 43, 71–90 (1990).
ADS Article Google Scholar
- 14.
Massol, H. & Koyaguchi, T. The effect of magma flow on nucleation of gas bubbles in a volcanic conduit. J. Volcanol. Geotherm. Res. 143, 69–88 (2005).
ADS CAS Article Google Scholar
- 15.
Mastin, L. G. & Ghiorso, M. S. A numerical program for steady-state flow of magma-gas mixtures through vertical eruptive conduits, (Department of the Interior, Washington DC, 2000).
- 16.
Barth, A. et al. Magma decompression rate correlates with explosivity at basaltic volcanoes – Constraints from water diffusion in olivine. J. Volcanol. Geother. Res. 387, 106664 (2019).
CAS Article Google Scholar
- 17.
Toramaru, A. BND (bubble number density) decompression rate meter for explosive volcanic eruptions. J. Volcanol. Geother. Res. 154, 303–316 (2006).
ADS CAS Article Google Scholar
- 18.
Navon, O. and Lyakhovsky, V. Vesiculation processes in silicic magmas. in The physics of explosive volcanic eruptions, (eds Gilbert, J. S. & Sparks, R. S. J.) 27–50 (Geological Society, London, Special Publications, Cambridge, UK, 1998).
- 19.
Gardner, J. E., Hajimirza, S., Webster, J. D. & Gonnermann, H. M. The impact of dissolved fluorine on bubble nucleation in hydrous rhyolite melts. Geochim. Cosmochim. Acta 226, 174–181 (2018).
ADS CAS Article Google Scholar
- 20.
Hurwitz, S. & Navon, O. Bubble nucleation in rhyolitic melts: experiments at high pressure, temperature, and water content. Earth Planet. Sci. Lett. 122, 267–280 (1994).
ADS CAS Article Google Scholar
- 21.
Gardner, J. E. & Denis, M. Heterogeneous bubble nucleation on Fe-Ti oxide crystals in high-silica rhyolitic melts. Geochim. Cosmochim. Acta 68, 3587–3597 (2004).
ADS CAS Article Google Scholar
- 22.
Larsen, J. F. Heterogeneous bubble nucleation and disequilibrium H2O exsolution in Vesuvius K-phonolite melts. J. Volcanol. Geother. Res. 175, 278–288 (2008).
ADS CAS Article Google Scholar
- 23.
Cluzel, N., Laporte, D., Provost, A. & Kannewischer, I. Kinetics of heterogeneous bubble nucleation in rhyolitic melts: implications for the number density of bubbles in volcanic conduits and for pumice textures. Contrib. Mineral. Petrol. 156, 745–763 (2008).
ADS CAS Article Google Scholar
- 24.
Mujin, M., Nakamura, M. & Miyake, A. Eruption style and crystal size distributions: crystallization of groundmass nanolites in the 2011 Shinmoedake eruption. Am. Mineral. 102, 2367–2380 (2017).
ADS Article Google Scholar
- 25.
Schlinger, C. M., Rosenbaum, J. G. & Veblen, D. R. Fe-oxide microcrystals in welded tuff from southern Nevada: origin of remanence carriers by precipitation in volcanic glass. Geology 16, 556–559 (1988).
ADS CAS Article Google Scholar
- 26.
Di Genova, D. A. et al. A compositional tipping point governing the mobilization and eruption style of rhyolitic magma. Nature 552, 235–238 (2017).
ADS PubMed Article CAS Google Scholar
- 27.
Di Genova, D., Caracciolo, A. & Kolzenburg, S. Measuring the degree of "nanotilization" of volcanic glasses: understanding syn-eruptive processes recorded in melt inclusions. Lithos 318-319, 209–218 (2018).
ADS Article CAS Google Scholar
- 28.
Gardner, J. E., Hilton, M. & Carroll, M. R. Experimental constraints on degassing of magma: isothermal bubble growth during continuous decompression from high pressure. Earth Planet. Sci. Lett. 168, 201–218 (1999).
ADS CAS Article Google Scholar
- 29.
Slezin, Y. B. The mechanism of volcanic eruptions (a steady state approach). J. Volcanol. Geother. Res. 122, 7–50 (2003).
ADS CAS Article Google Scholar
- 30.
Chernov, A. A., Kedrinsky, V. K. & Pil'nik, A. A. Kinetics of gas bubble nucleation and growth in magmatic melt at its rapid decompression. Phys. Fluids 26, (2014).
- 31.
Hirth, J. P., Pound, G. M. & Pierre, G. R. S. Bubble nucleation. Metall. Trans. 1, 939–945 (1969).
Google Scholar
- 32.
Mangan, M. T. & Sisson, T. Evolution of melt-vapor surface tension in silicic volcanic systems: experiments with hydrous melts. J. Geophy. Res. 110, B01202 (2005).
ADS Article CAS Google Scholar
- 33.
Bagdassarov, N., Dorfman, A. & Dingwell, D. B. Effect of alkalis, phosphorus, and water on the surface tension of haplogranite melt. American Mineralogist 85, 33–40 (2000).
ADS CAS Article Google Scholar
- 34.
Tolman, R. C. The effect of droplet size on surface tension. J. Chem. Phys. 17, 333–337 (1949).
ADS CAS Article Google Scholar
- 35.
Liu, Y., Zhang, Y. & Behrens, H. Solubility of H2O in rhyolitic melts at low pressures and a new empirical model for mixed H2O–CO2 solubility in rhyolitic melts. J. Volcanol. Geotherm. Res. 143, 219–235 (2005).
ADS CAS Article Google Scholar
- 36.
Papale, P. Strain-induced magma fragmentation in explosive eruptions. Nature 397, 425–428 (1999).
ADS CAS PubMed Article Google Scholar
- 37.
Zhang, Y. & Behrens, H. H2O diffusion in rhyolitic melts and glasses. Chem. Geol. 169, 243–262 (2000).
ADS CAS Article Google Scholar
- 38.
Holloway, J. R. Thermodynamics in Geology 161–181 (Springer Netherlands, Dordrecht, Netherlands, 1977).
Google Scholar
- 39.
Ochs, F. A. & Lange, R. A. The density of hydrous magmatic liquids. Science 283, 1314–1317 (1999).
ADS CAS Article PubMed Google Scholar
- 40.
Carey, R. J., Houghton, B. F. & Thordarson, T. Abrupt shifts between wet and dry phases of the 1875 eruption of Askja Volcano: Microscopic evidence for macroscopic dynamics. J. Volcanol. Geotherm. Res. 184, 256–270 (2009).
ADS CAS Article Google Scholar
- 41.
Sigurdsson, H. & Sparks, R. S. J. Petrology of Rhyolitic and mixed magma ejecta from the 1875 eruption of Askja, Iceland. J. Petrol. 22, 41–84 (1981).
ADS CAS Article Google Scholar
- 42.
Alfano, F., Bonadonna, C. & Gurioli, L. Insights into eruption dynamics from textural analysis: the case of the May, 2008, Chaitén eruption. Bull. Volcanol. 74, 2095–2108 (2012).
ADS Article Google Scholar
- 43.
Castro, J. M. & Dingwell, D. B. Rapid ascent of rhyolitic magma at Chaitén Volcano, Chile. Nature 461, 780–783 (2009).
ADS CAS PubMed Article Google Scholar
- 44.
Klug, C., Cashman, K. V. & Bacon, C. Structure and physical characteristics of pumice from the climactic eruption of Mount Mazama (Crater Lake), Oregon. Bull.Volcanol. 64, 486–501 (2002).
ADS Article Google Scholar
- 45.
Bacon, C. R. & Druitt, T. H. Compositional evolution of the zoned calcalkaline magma chamber of Mount Mazama, Crater Lake, Oregon. Contrib. Mineral. Petrol. 98, 224–256 (1988).
ADS CAS Article Google Scholar
- 46.
Carey, S., Sigurdsson, H., Gardner, J. E. & Cristwell, W. Variations in column height and chamber during the May 18, 1980 eruption of Mt. St. Helens. J. Volcanol. Geotherm. Res. 43, 99–112 (1990).
ADS Article Google Scholar
- 47.
Rutherford, M. J., Sigurdsson, H., Carey, S. & Davis, A. The May 18, 1980, eruption of Mount St. Helens. 1. Melt composition and experimental phase equilibria. J. Geophys. Res. 90, 2929–2947 (1985).
ADS CAS Article Google Scholar
- 48.
Klug, C. & Cashman, K. V. Vesiculation of May 18, 1980, Mount St. Helens magma. Geology 22, 468 (1994).
ADS Article Google Scholar
- 49.
Adams, N. K., Houghton, B. F. & Hildreth, W. Abrupt transitions during sustained explosive eruptions: examples from the 1912 eruption of Novarupta, Alaska. Bull. Volcanol. 69, 189–206 (2006).
ADS Article Google Scholar
- 50.
Hammer, J. E., Rutherford, M. J. & Hildreth, W. Magma storage prior to the 1912 eruption at Novarupta, Alaska. Contrib. Mineral. Petrol. 144, 144–162 (2002).
ADS CAS Article Google Scholar
- 51.
Polacci, M., Papale, P. & Rosi, M. Textural heterogeneities in pumices from the climactic eruption of Mount Pinatubo, 15 June 1991, and implications for magma ascent dynamics. Bull. Volcanol. 63, 83–97 (2001).
ADS Article Google Scholar
- 52.
Hammer, J. E. & Rutherford, M. J. An experimental study of the kinetics of decompression-induced crystallization in silicic melt. J. Geophys. Res. 107, ECV 8–1–ECV 8–24 (2002).
Article CAS Google Scholar
- 53.
Houghton, B. F. Diverse patterns of ascent, degassing, and eruption of rhyolite magma during the 1.8 ka Taupo eruption, New Zealand: evidence from clast vesicularity. J. Volcanol. Geotherm. Res. 195, 31–47 (2010).
ADS CAS Article Google Scholar
- 54.
Gardner, J. E. & Ketcham, R. A. Bubble nucleation in rhyolite and dacite melts: temperature dependence of surface tension. Contrib. Mineral. Petrol. 162, 929–943 (2011).
ADS CAS Article Google Scholar
- 55.
Gonnermann, H. M. & Gardner, J. E. Homogeneous bubble nucleation in rhyolitic melt: experiments and nonclassical theory. Geochem. Geophys. Geosyst. 14, 4758–4773 (2013).
ADS CAS Article Google Scholar
- 56.
Giachetti, T. Bubble Coalescence and Percolation threshold in expanding Rhyolitic Magma. Geochem. Geophys. Geosyst. 20, 1054–1074 (2019).
ADS Article Google Scholar
- 57.
Hamada, M., Laporte, D., Cluzel, N., Koga, K. T. & Kawamoto, T. Simulating bubble number density of rhyolitic pumices from Plinian eruptions: constraints from fast decompression experiments. Bull. Volcanol. 72, 735–746 (2010).
ADS Article Google Scholar
- 58.
Mourtada-Bonnefoi, C. C. & Laporte, D. Homogeneous bubble nucleation in rhyolitic magmas: an experimental study of the effect of H2O and CO2. J. Geophys. Res. 107, ECV 2–1–ECV 2–19 (2002).
Article Google Scholar
- 59.
Mourtada-Bonnefoi, C. C. & Laporte, D. Kinetics of bubble nucleation in a rhyolitic melt: an experimental study of the effect of ascent rate. Earth and Planet. Sci. Lett. 218, 521–537 (2004).
ADS CAS Article Google Scholar
- 60.
Humphreys, M. C. S., Menand, T., Blundy, J. D. & Klimm, K. Magma ascent rates in explosive eruptions: constraints from H2O diffusion in melt inclusions. Earth Planet. Sci. Lett. 270, 25–40 (2008).
ADS CAS Article Google Scholar
- 61.
Carey, S. & Sigurdsson, H. The May 18, 1980 eruption of Mount St. Helens: 2. Modeling of dynamics of the Plinian phase. J. Geophys. Res. 90, 2948 (1985).
ADS Article Google Scholar
- 62.
Papale, P. & Dobran, F. Magma flow along the volcanic conduit during the Plinian and pyroclastic flow phases of the May 18, 1980, Mount St. Helens eruption. J. Geophys. Res. 99, 4355–4373 (1994).
ADS Article Google Scholar
- 63.
Rutherford, M. J. & Hill, P. M. Magma ascent rates from amphibole breakdown: an experimental study applied to the 1980-1986 Mount St. Helens Eruptions. J. Geophys. Res. 98, 19667–19685 (1993).
ADS CAS Article Google Scholar
- 64.
Geschwind, C. H. & Rutherford, M. J. Crystallization of microlites during magma ascent: the fluid mechanics of 1980-1986 eruptions at Mount St. Helens. Bull. Volcanol. 57, 356–370 (1995).
ADS Article Google Scholar
- 65.
Anderson, A. T. Hourglass inclusions: theory and application to the Bishop Rhyolitic Tuff. Am. Mineral. 76, 530–547 (1991).
CAS Google Scholar
- 66.
Myers, M. L., Wallace, P. J., Wilson, C. J., Watkins, J. M. & Liu, Y. Ascent rates of rhyolitic magma at the onset of three caldera-forming eruptions. Am. Mineral. 103, 952–965 (2018).
ADS Article Google Scholar
- 67.
Charlier, B. L. Lithium concentration gradients in feldspar and quartz record the final minutes of magma ascent in an explosive supereruption. Earth Planet. Sci. Lett. 319-320, 218–227 (2012).
ADS CAS Article Google Scholar
- 68.
Liu, Y., Anderson, A. T. & Wilson, C. J. Melt pockets in phenocrysts and decompression rates of silicic magmas before fragmentation. J. Geophys. Res. 112, 1–12 (2007).
Google Scholar
Download references
Acknowledgements
This work was supported by the National Science Foundation grants EAR-1348072 and EAR-1348050. We thank Mattia de' Michieli Vitturi, Michihiko Nakamura, and one anonymous reviewer for their valuable suggestions and comments.
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Madison Myers, Michihiko Nakamura and Mattia de' Michieli Vitturi for their contribution to the peer review of this work.
Publisher's note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
Reprints and Permissions
About this article
Cite this article
Hajimirza, S., Gonnermann, H.M. & Gardner, J.E. Reconciling bubble nucleation in explosive eruptions with geospeedometers. Nat Commun 12, 283 (2021). https://doi.org/10.1038/s41467-020-20541-1
Download citation
-
Received:
-
Accepted:
-
Published:
-
DOI : https://doi.org/10.1038/s41467-020-20541-1
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.
Modeling Volcanic Processes The Physics And Mathematics Of Volcanism Pdf
Source: https://www.nature.com/articles/s41467-020-20541-1
Posted by: swanmencir.blogspot.com

0 Response to "Modeling Volcanic Processes The Physics And Mathematics Of Volcanism Pdf"
Post a Comment